banner



Home  ›  how to find volume of a triangular prism

how to find volume of a triangular prism

Written By Sunday, October 31, 2021 Add Comment Edit
Uniform triangular prism
Triangular prism.png
Type Prismatic uniform polyhedron
Elements F = 5, E = 9
V = 6 (χ = 2)
Faces by sides 3{4}+2{3}
Schläfli symbol t{2,3} or {3}×{}
Wythoff symbol 2 3 | 2
Coxeter diagram CDel node 1.png CDel 2.png CDel node 1.png CDel 3.png CDel node.png
Symmetry group D3h, [3,2], (*322), order 12
Rotation group D3, [3,2]+, (322), order 6
References U76(a)
Dual Triangular dipyramid
Properties convex
Triangular prism vertfig.svg
Vertex figure
4.4.3

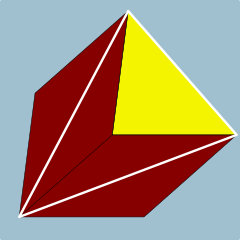
3D model of a (uniform) triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

Equivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle.

As a semiregular (or uniform) polyhedron [edit]

A right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol t{2,3}. Alternately it can be seen as the Cartesian product of a triangle and a line segment, and represented by the product, The dual of a triangular prism is a triangular bipyramid.

The symmetry group of a right 3-sided prism with triangular base is D3h of order 12. The rotation group is D3 of order 6. The symmetry group does not contain inversion.

Volume [edit]

The volume of any prism is the product of the area of the base and the distance between the two bases. In this case the base is a triangle so we simply need to compute the area of the triangle and multiply this by the length of the prism:

V = b h l 2 , {\displaystyle V={\frac {bhl}{2}},}

where b is the length of one side of the triangle, h is the length of an altitude drawn to that side, and l is the distance between the triangular faces.

Truncated triangular prism [edit]

A truncated right triangular prism has one triangular face truncated (planed) at an oblique angle.[1]

TruncatedTriangularPrism.png

The volume of a truncated triangular prism with base area A and the three heights h 1, h 2, and h 3 is determined by[2]

V = A ( h 1 + h 2 + h 3 ) 3 . {\displaystyle V={\frac {A(h_{1}+h_{2}+h_{3})}{3}}.}

Facetings [edit]

There are two full D3h symmetry facetings of a triangular prism, both with 6 isosceles triangle faces, one keeping the original top and bottom triangles, and one the original squares. Two lower C3v symmetry facetings have one base triangle, 3 lateral crossed square faces, and 3 isosceles triangle lateral faces.

Convex Facetings
D3h symmetry C3v symmetry
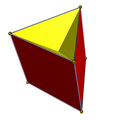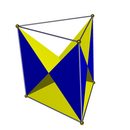Triangular prism.png FacetedTriangularPrism2.png FacetedTriangularPrism.png FacetedTriangularPrism3.png FacetedTriangularPrism4.png
2 {3}
3 {4} 		3 {4}
6 ( ) v { } 		2 {3}
6 ( ) v { } 		1 {3}
3 t'{2}
6 ( ) v { } 		1 {3}
3 t'{2}
3 ( ) v { }

Related polyhedra and tilings [edit]

Family of uniform n-gonal prisms
  • v
  • t
  • e
Prism name Digonal prism (Trigonal)
Triangular prism 		(Tetragonal)
Square prism 		Pentagonal prism Hexagonal prism Heptagonal prism Octagonal prism Enneagonal prism Decagonal prism Hendecagonal prism Dodecagonal prism ... Apeirogonal prism
Polyhedron image Yellow square.gif Triangular prism.png Tetragonal prism.png Pentagonal prism.png Hexagonal prism.png Prism 7.png Octagonal prism.png Prism 9.png Decagonal prism.png Hendecagonal prism.png Dodecagonal prism.png ...
Spherical tiling image Tetragonal dihedron.png Spherical triangular prism.png Spherical square prism.png Spherical pentagonal prism.png Spherical hexagonal prism.png Spherical heptagonal prism.png Spherical octagonal prism.png Spherical decagonal prism.png Plane tiling image Infinite prism.svg
Vertex config. 2.4.4 3.4.4 4.4.4 5.4.4 6.4.4 7.4.4 8.4.4 9.4.4 10.4.4 11.4.4 12.4.4 ... ∞.4.4
Coxeter diagram CDel node 1.png CDel 2.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 3.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 4.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 5.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 6.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 7.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 8.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 9.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 10.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 11.png CDel node.png CDel 2.png CDel node 1.png CDel node 1.png CDel 12.png CDel node.png CDel 2.png CDel node 1.png ... CDel node 1.png CDel infin.png CDel node.png CDel 2.png CDel node 1.png
Family of convex cupolae
  • v
  • t
  • e
n 2 3 4 5 6
Name {2} || t{2} {3} || t{3} {4} || t{4} {5} || t{5} {6} || t{6}
Cupola Triangular prism wedge.png
Digonal cupola 		Triangular cupola.png
Triangular cupola 		Square cupola.png
Square cupola 		Pentagonal cupola.png
Pentagonal cupola 		Hexagonal cupola flat.png
Hexagonal cupola
(Flat)
Related
uniform
polyhedra 		Triangular prism
CDel node 1.png CDel 2.png CDel node.png CDel 3.png CDel node 1.png 		Cubocta-
hedron
CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png 		Rhombi-
cubocta-
hedron
CDel node 1.png CDel 4.png CDel node.png CDel 3.png CDel node 1.png 		Rhomb-
icosidodeca-
hedron
CDel node 1.png CDel 5.png CDel node.png CDel 3.png CDel node 1.png 		Rhombi-
trihexagonal
tiling
CDel node 1.png CDel 6.png CDel node.png CDel 3.png CDel node 1.png

Symmetry mutations [edit]

This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.

*n32 symmetry mutation of truncated tilings: t{n,3}
  • v
  • t
  • e
Symmetry
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paraco. Noncompact hyperbolic
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3] 		[12i,3] [9i,3] [6i,3]
Truncated
figures 		Spherical triangular prism.png Uniform tiling 332-t01-1-.png Uniform tiling 432-t01.png Uniform tiling 532-t01.png Uniform tiling 63-t01.svg Truncated heptagonal tiling.svg H2-8-3-trunc-dual.svg H2 tiling 23i-3.png H2 tiling 23j12-3.png H2 tiling 23j9-3.png H2 tiling 23j6-3.png
Symbol t{2,3} t{3,3} t{4,3} t{5,3} t{6,3} t{7,3} t{8,3} t{∞,3} t{12i,3} t{9i,3} t{6i,3}
Triakis
figures 		Spherical trigonal bipyramid.png Spherical triakis tetrahedron.png Spherical triakis octahedron.png Spherical triakis icosahedron.png Tiling Dual Semiregular V3-12-12 Triakis Triangular.svg Order-7 triakis triangular tiling.svg H2-8-3-kis-primal.svg Ord-infin triakis triang til.png
Config. V3.4.4 V3.6.6 V3.8.8 V3.10.10 V3.12.12 V3.14.14 V3.16.16 V3.∞.∞

This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

*n32 symmetry mutation of expanded tilings: 3.4.n.4
Symmetry
*n32
[n,3] 		Spherical Euclid. Compact hyperb. Paracomp.
*232
[2,3] 		*332
[3,3] 		*432
[4,3] 		*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3]... 		*∞32
[∞,3]
Figure Spherical triangular prism.png Uniform tiling 332-t02.png Uniform tiling 432-t02.png Uniform tiling 532-t02.png Uniform polyhedron-63-t02.png Rhombitriheptagonal tiling.svg H2-8-3-cantellated.svg H2 tiling 23i-5.png
Config. 3.4.2.4 3.4.3.4 3.4.4.4 3.4.5.4 3.4.6.4 3.4.7.4 3.4.8.4 3.4.∞.4

Compounds [edit]

There are 4 uniform compounds of triangular prisms:

Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.

Honeycombs [edit]

There are 9 uniform honeycombs that include triangular prism cells:

Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb

[edit]

The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −121.

k21 figures in n dimensional
Space Finite Euclidean Hyperbolic
En 3 4 5 6 7 8 9 10
Coxeter
group 		E3=A2A1 E4=A4 E5=D5 E6 E7 E8 E9 = E ~ 8 {\displaystyle {\tilde {E}}_{8}} = E8 + E10 = T ¯ 8 {\displaystyle {\bar {T}}_{8}} = E8 ++
Coxeter
diagram 		CDel node.png CDel 3.png CDel node 1.png CDel 2.png CDel node 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch 10.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea 1.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel branch.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea.png CDel 3a.png CDel nodea 1.png
Symmetry [3−1,2,1] [30,2,1] [31,2,1] [32,2,1] [33,2,1] [34,2,1] [35,2,1] [36,2,1]
Order 12 120 1,920 51,840 2,903,040 696,729,600 ∞
Graph Triangular prism.png 4-simplex t1.svg Demipenteract graph ortho.svg E6 graph.svg E7 graph.svg E8 graph.svg - -
Name −121 021 121 221 321 421 521 621

Four dimensional space [edit]

The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:

Four dimensional polytopes with triangular prisms
Tetrahedral prism
CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node.png CDel 2.png CDel node 1.png 		Octahedral prism
CDel node 1.png CDel 3.png CDel node.png CDel 4.png CDel node.png CDel 2.png CDel node 1.png 		Cuboctahedral prism
CDel node.png CDel 3.png CDel node 1.png CDel 4.png CDel node.png CDel 2.png CDel node 1.png 		Icosahedral prism
CDel node 1.png CDel 3.png CDel node.png CDel 5.png CDel node.png CDel 2.png CDel node 1.png 		Icosidodecahedral prism
CDel node.png CDel 3.png CDel node 1.png CDel 5.png CDel node.png CDel 2.png CDel node 1.png 		Truncated dodecahedral prism
CDel node.png CDel 3.png CDel node 1.png CDel 5.png CDel node 1.png CDel 2.png CDel node 1.png
Tetrahedral prism.png Octahedral prism.png Cuboctahedral prism.png Icosahedral prism.png Icosidodecahedral prism.png Truncated dodecahedral prism.png
Rhomb-icosidodecahedral prism
CDel node 1.png CDel 3.png CDel node.png CDel 5.png CDel node 1.png CDel 2.png CDel node 1.png 		Rhombi-cuboctahedral prism
CDel node 1.png CDel 3.png CDel node.png CDel 4.png CDel node 1.png CDel 2.png CDel node 1.png 		Truncated cubic prism
CDel node.png CDel 3.png CDel node 1.png CDel 4.png CDel node 1.png CDel 2.png CDel node 1.png 		Snub dodecahedral prism
CDel node h.png CDel 5.png CDel node h.png CDel 3.png CDel node h.png CDel 2.png CDel node 1.png 		n-gonal antiprismatic prism
CDel node h.png CDel n.png CDel node h.png CDel 2x.png CDel node h.png CDel 2.png CDel node 1.png
Rhombicosidodecahedral prism.png Rhombicuboctahedral prism.png Truncated cubic prism.png Snub dodecahedral prism.png Square antiprismatic prism.png
Cantellated 5-cell
CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Cantitruncated 5-cell
CDel node 1.png CDel 3.png CDel node 1.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Runcinated 5-cell
CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png 		Runcitruncated 5-cell
CDel node 1.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png 		Cantellated tesseract
CDel node 1.png CDel 4.png CDel node.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Cantitruncated tesseract
CDel node 1.png CDel 4.png CDel node 1.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Runcinated tesseract
CDel node 1.png CDel 4.png CDel node.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png 		Runcitruncated tesseract
CDel node 1.png CDel 4.png CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png
4-simplex t02.svg 4-simplex t012.svg 4-simplex t03.svg 4-simplex t013.svg 4-cube t02.svg 4-cube t012.svg 4-cube t03.svg 4-cube t013.svg
Cantellated 24-cell
CDel node 1.png CDel 3.png CDel node.png CDel 4.png CDel node 1.png CDel 3.png CDel node.png 		Cantitruncated 24-cell
CDel node 1.png CDel 3.png CDel node 1.png CDel 4.png CDel node 1.png CDel 3.png CDel node.png 		Runcinated 24-cell
CDel node 1.png CDel 3.png CDel node.png CDel 4.png CDel node.png CDel 3.png CDel node 1.png 		Runcitruncated 24-cell
CDel node 1.png CDel 3.png CDel node 1.png CDel 4.png CDel node.png CDel 3.png CDel node 1.png 		Cantellated 120-cell
CDel node 1.png CDel 5.png CDel node.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Cantitruncated 120-cell
CDel node 1.png CDel 5.png CDel node 1.png CDel 3.png CDel node 1.png CDel 3.png CDel node.png 		Runcinated 120-cell
CDel node 1.png CDel 5.png CDel node.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png 		Runcitruncated 120-cell
CDel node 1.png CDel 5.png CDel node 1.png CDel 3.png CDel node.png CDel 3.png CDel node 1.png
24-cell t02 F4.svg 24-cell t012 F4.svg 24-cell t03 F4.svg 24-cell t013 F4.svg 120-cell t02 H3.png 120-cell t012 H3.png 120-cell t03 H3.png 120-cell t013 H3.png

See also [edit]

  • Wedge (geometry)

References [edit]

  1. ^ Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.
  2. ^ "Volume of truncated prism". Mathematics Stack Exchange . Retrieved 9 July 2019.
  • Weisstein, Eric W. "Triangular prism". MathWorld.
  • Interactive Polyhedron: Triangular Prism
  • Surface area and volume of a triangular prism

how to find volume of a triangular prism

Source: https://en.wikipedia.org/wiki/Triangular_prism

Posted by: redfieldfoublinges.blogspot.com

0 Response to "how to find volume of a triangular prism"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel